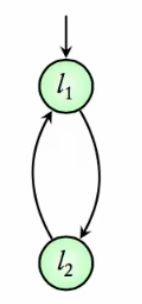
MODULE main
VAR
location : {l1, l2};
ASSIGN
init(location) := l1;
next(location) := case
location = l1 : l2;
location = l2 : l1;
esac;
Notes based on the course on Model Checking by Prof. B. Srivathsan (CMI). Lecture Video
NuSMV is a symbolic model checker used to describe and verify finite state transition systems.
A transition system in NuSMV is specified by defining:
Scenario: A simple system with two states l1 and l2. The initial state is l1, and transitions go from l1 to l2 and back from l2 to l1.

MODULE main
VAR
location : {l1, l2};
ASSIGN
init(location) := l1;
next(location) := case
location = l1 : l2;
location = l2 : l1;
esac;
Assuming the above code is saved in a file named intro_demo.smv, follow these steps in the terminal:
NuSMV -int
This starts NuSMV in interactive mode. Within NuSMV, enter:
read_model -i intro_demo.smv
flatten_hierarchy
encode_variables
build_model
read_model loads the model file.flatten_hierarchy processes module hierarchies.encode_variables encodes variables for model checking.build_model completes the model construction.Alternatively, do
NuSMV -int intro_demo.smv, thengo.
pick_state -ilocation = l1simulate -i -k 10
location = l1 and location = l2.print_reachable_states -v
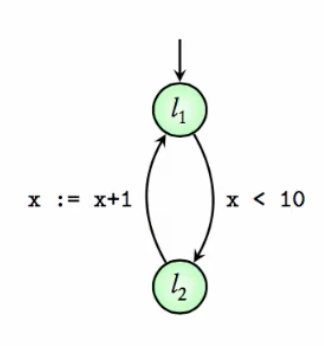
location = l1 and location = l2.Now, consider a system with:
States l1 and l2.
An integer variable x ranging from 0 to 100.
Transition from l1 to l2 allowed only if x < 10.
When moving from l2 to l1, x increments by 1 (bounded by 100). NuSMV supports only bounded variables.
MODULE main
VAR
location : {l1, l2};
x : 0..100;
ASSIGN
init(location) := l1;
init(x) := 0;
next(location) := case
(location = l1) & (x < 10) : l2;
(location = l2) : l1;
TRUE : location; # Default: don't change location
esac;
next(x) := case
(location = l1) : x;
(location = l2) & (x < 100) : x + 1;
TRUE : x;
esac;
To exit the current session use the command quit
Load and build the model as before:
read_model -i pg_demo.smv
flatten_hierarchy
encode_variables
build_model
or
NuSMV -int pg_demo.smv
go
Check the initial state:
pick_state -i
Expected:
location = l1, x = 0simulate -i -k 15
location alternates and x increments when transitioning from l2 to l1.print_reachable_states -v
location and x values.Example with: Boolean variable request,
Enum variable status is either ready or busy
status = ready, request unspecified (hence two initial states)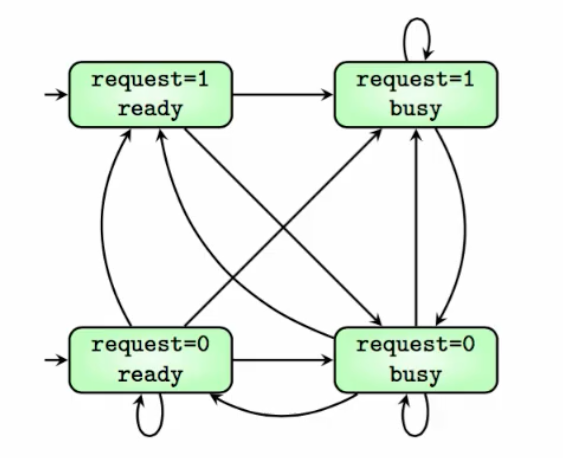
MODULE main
VAR
request : boolean;
status : {ready, busy};
ASSIGN
init(status) := ready;
next(status) := case
request : busy;
TRUE : {ready, busy};
esac;
Loading and build:
NuSMV -int request_busy_demo.smv
go
See all states (4 total):
print_reachable_states -v
Simulate starting from an initial state
pick_state -i to select an initial state
simulate -i -k 3
You can observe transitions between various request and status values. You also have to choose the next transitions to take.
Example Execution 1:
Example Execution 2:
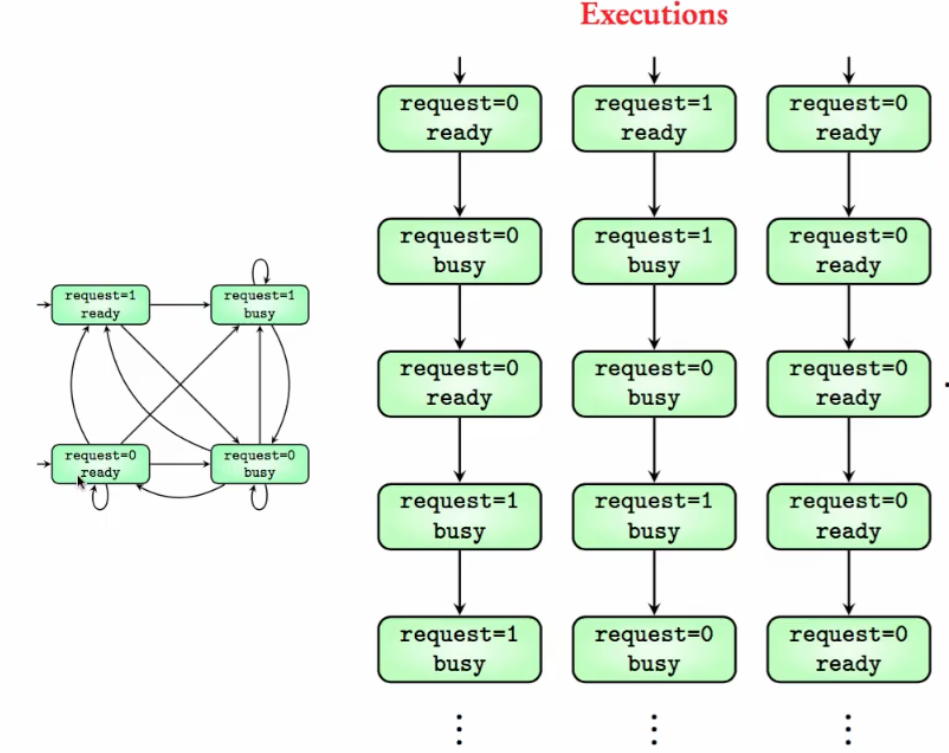
A transition system satisfies a requirement if all its executions satisfy the requirement.
NuSMV supports temporal logic specifications, especially LTL (Linear Temporal Logic), to verify properties such as:
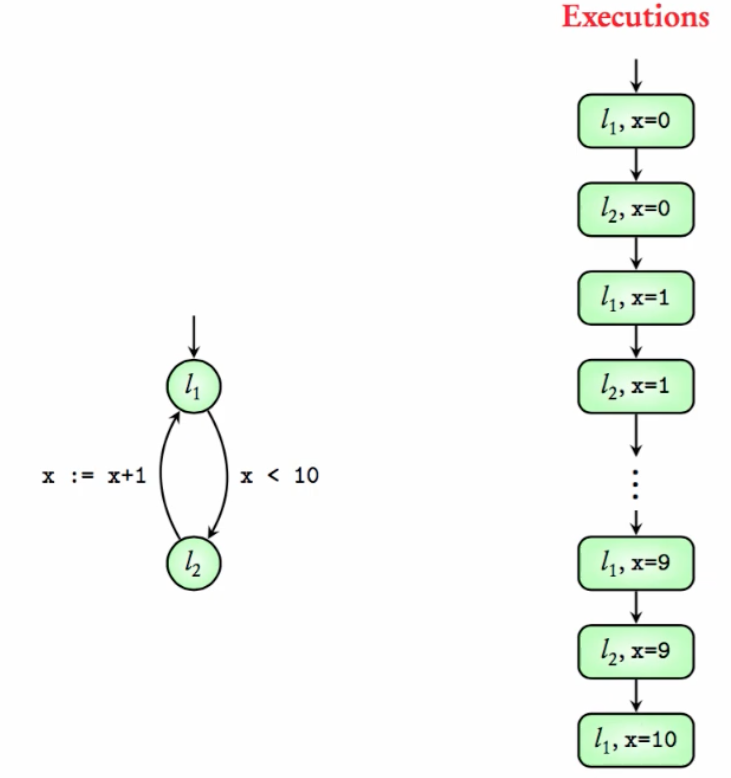
G(x>=0) is true in EE 1. G(request=0) is false in EE 2 but is true for the third execution in EE 2.F(request=1) is false in EE 2 but true for the first and second executions in EE 2.Example 1: Check if
x >= 0always holds in pg_demo.smv
NuSMV -int pg_demo.smv
go
check_ltlspec -p "G (x >= 0)"
NuSMV output will confirm whether the specification is true.
Example 2: Check if
request = FALSEalways holds in request_busy_demo.smv
NuSMV -int request_busy_demo.smv
go
check_ltlspec -p "G (request = FALSE)"
F(request=1)isfalsein EE 2 because of the third execution.
NuSMV will state that the specification is false and provide a counterexample execution.
Example 3: Check if eventually
x >= 5holds in pg_demo.smv (see Example Execution 1).
NuSMV -int pg_demo.smv
go
check_ltlspec -p "F (x >= 5)"
Expected output: Specification F x >= 5 is true
Example 4: Check if whenever
requestistrue,statuseventually becomesbusyin request_busy_demo.smv
NuSMV -int request_busy_demo.smv
go
check_ltlspec -p "G (request = TRUE -> F (status = busy))"
NuSMV should confirm this property is true. This is not easy to check by just looking at the transition system.
VAR and ASSIGN blocks in NuSMV.init.next with case statements.check_ltlspec.This lecture prepares you to model systems and formally verify their properties using NuSMV.
In this lecture, we explore how to describe hardware circuits using the NuSMV tool. Building on prior knowledge of modeling simple transition systems, we delve into three parts:
x and r (both boolean).y = NOT of XOR of x and r.r: XOR of current x and r.x is nondeterministic (can be either 0 or 1).r is false; x can start as true or false.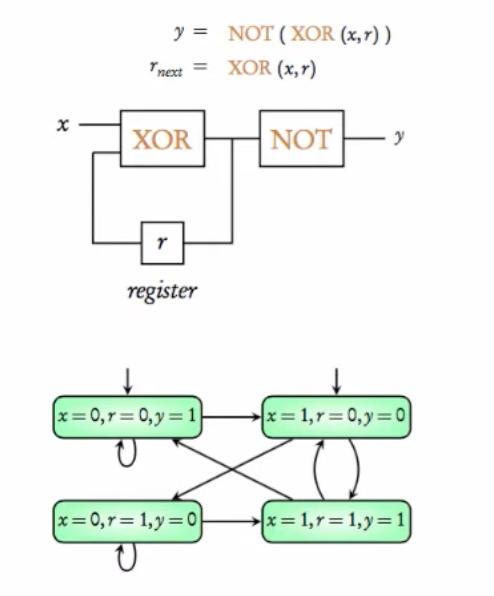
MODULE main
VAR
x : boolean;
r : boolean;
DEFINE
y := !(x xor r);
ASSIGN
init(r) := FALSE;
next(r) := x xor r;
x and r declared in VAR block.r's next value is assigned with a delay using next(r) := x xor r.y depends immediately on current values; modeled using DEFINE y := !(x xor r).y is not declared in VAR because it does not affect state space.x * 2 for r).The command NuSMV -int circuit_demo1.smv launches interactive mode.
Use the command go instead of read_model flatten_heirarchy, encode_variables and build_model -- same functionality.
Using print_reachable_states -v shows the 4 possible states.
Using print_fair_transitions -v shows all the 8 possible transitions.
Simulation illustrates how r evolves over steps, while y updates immediately.
Each state has two possible successors due to nondeterministic x.
pick_state -i to pick an initial state.
simulate -i -k 5 simulates the model for five steps.
Use of DEFINE is crucial for outputs depending on current state without delay.
State space is determined solely by variables in VAR.
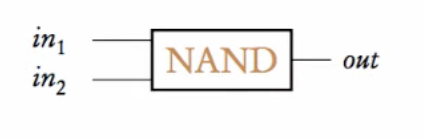
MODULE main
VAR
in1 : boolean;
in2 : boolean;
DEFINE
out := !(in1 & in2);
NAND Gate With Zero Delay
Inputs: in1, in2 (boolean).
Output: out = ! (in1 & in2), defined with zero delay.
No initial states defined; all 4 input combinations are initial.
Transitions are unconstrained; any state can transition to any other.
NuSMV -int nand_demo1.smv followed by go to load the model.print_reachable_states -v to see the set of reachable states.pick_state -i Since we have not defined any initial state, any state can be initial.simulate -i 5 Simulates the model for five steps. Here, all transitions are possible.
out declared as a boolean variable with initial value true.out assigned as NAND of current inputs: next(out) := !(in1 & in2);.in1 and in2 remain nondeterministic.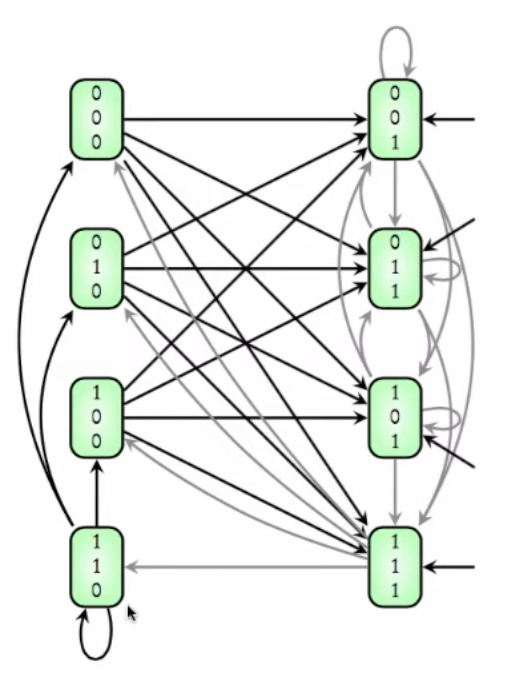
MODULE main
VAR
in1 : boolean;
in2 : boolean;
out : boolean;
ASSIGN
init(out) := TRUE;
next(out) := !(in1 & in2);
NuSMV -int nand_demo2.smv followed by go to load the model.print_reachable_states -v to see all the reachable states.pick_state -i to pick an initial state.simulate -i -k 5 to simulate for 5 steps.out = TRUE combined with all input values.NAND module nand2 with inputs in1, in2 and output out.out is updated with unit delay.MODULE nand2(in1, in2)
VAR
out : boolean;
ASSIGN
init(out) := TRUE;
next(out) := !(in1 & in2);
MODULE main
VAR
input1 : boolean;
input2 : boolean;
q : nand2(input1, input2);
NuSMV -int nand_demo3.smv, go
print_reachable_states -v :
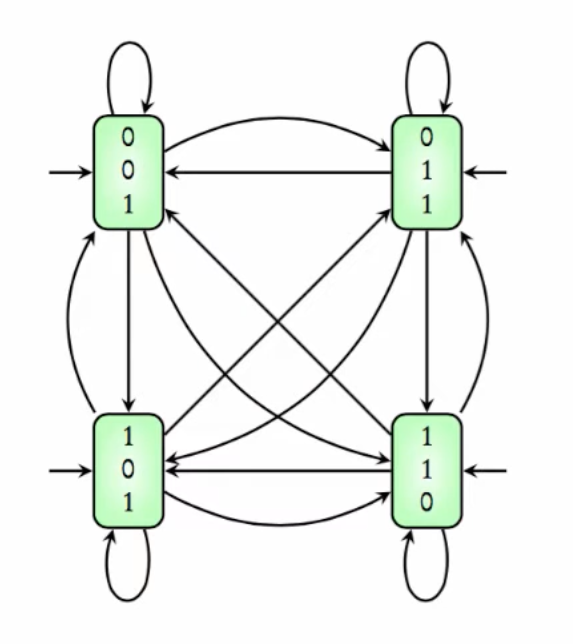
State space consists of input1, input2, and q.out.
Number of states: 8.
pick_state -i to pick initial state.
simulate -i -k 3 to simulate a run for 3 steps.
Modules becomes more useful while reusing components.
Instantiate two NAND modules q1 and q2 with inputs (x1, x2) and (y1, y2).
Output computed as XOR of q1.out and q2.out.
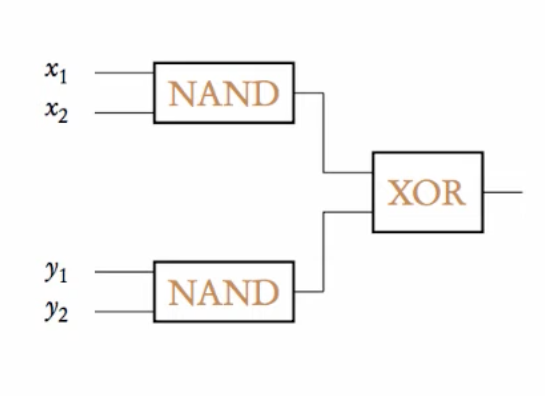
MODULE main
VAR
x1 : boolean; x2 : boolean;
y1 : boolean; y2 : boolean;
q1 : nand2(x1, x2);
q2 : nand2(y1, y2);
DEFINE
fout := q1.out xor q2.out;
MODULE nand2(in1, in2)
VAR
out : boolean;
ASSIGN
init(out) := TRUE;
next(out) := !(in1 & in2);
x1, x2, y1, y2, q1.out, q2.out.Two NAND gates connected in a feedback loop. Inputs x and y are boolean. Two variables q1 and q2 of nand2 type are instantiated with interdependent inputs.
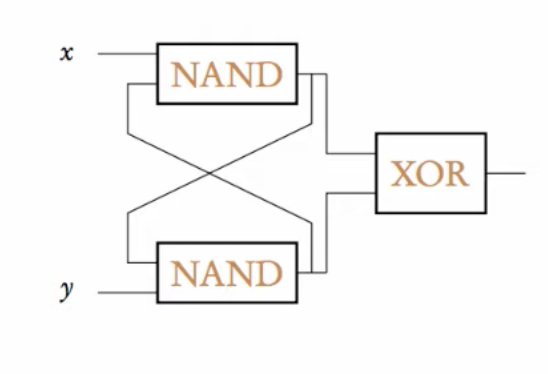
MODULE main
VAR
x : boolean;
y : boolean;
q1 : nand2(x, q2.out);
q2 : nand2(q1.out, y);
DEFINE
fout := q1.out xor q2.out;
MODULE nand2(in1, in2)
VAR
out : boolean;
ASSIGN
init(out) := TRUE;
next(out) := !(in1 & in2);
Inputs: x, y.
Variables: q1 takes (x, q2.out), q2 takes (q1.out, y).
Feedback loop between two NAND gates.
NuSMV -int nand_demo4.smv, go to load the model.
print_reachable_states -v
Number of states: 16 (2⁴).
Initial states: Both q1.out and q2.out start as TRUE.
pick_state -i to pick an initial state.
Next states computed synchronously using NAND of inputs.
x, y, q1.out, q2.out).q1.out and q2.out are TRUE as per module definition.NAND on current inputs.q1 and q2 creates complex state transitions.NuSMV -int nand-demo5.smv
go
print_reachable_states -v
pick_state -i
simulate -i k 5
value (bit), carryout (boolean).
carryout defined as carryin & value.value XOR carryin.
bit0 carryin is always TRUE.
bit1 and bit2 carryin depend on previous bit's carryout.
This constructs a synchronous 3-bit binary counter.
FALSE.
Each step updates all bits simultaneously.
The counter counts from 000 to 111 and wraps around.
Demonstrates synchronous composition: all modules update in lockstep.VAR define the state space; outputs dependent on current state can be modeled with DEFINE.next(variable) captures unit delay behavior.We cover modeling synchronous and asynchronous parallel systems, mutual exclusion, and concurrent programs using NuSMV. We explore examples with traffic lights, mutual exclusion for shared resources, and concurrent programs manipulating a shared variable.
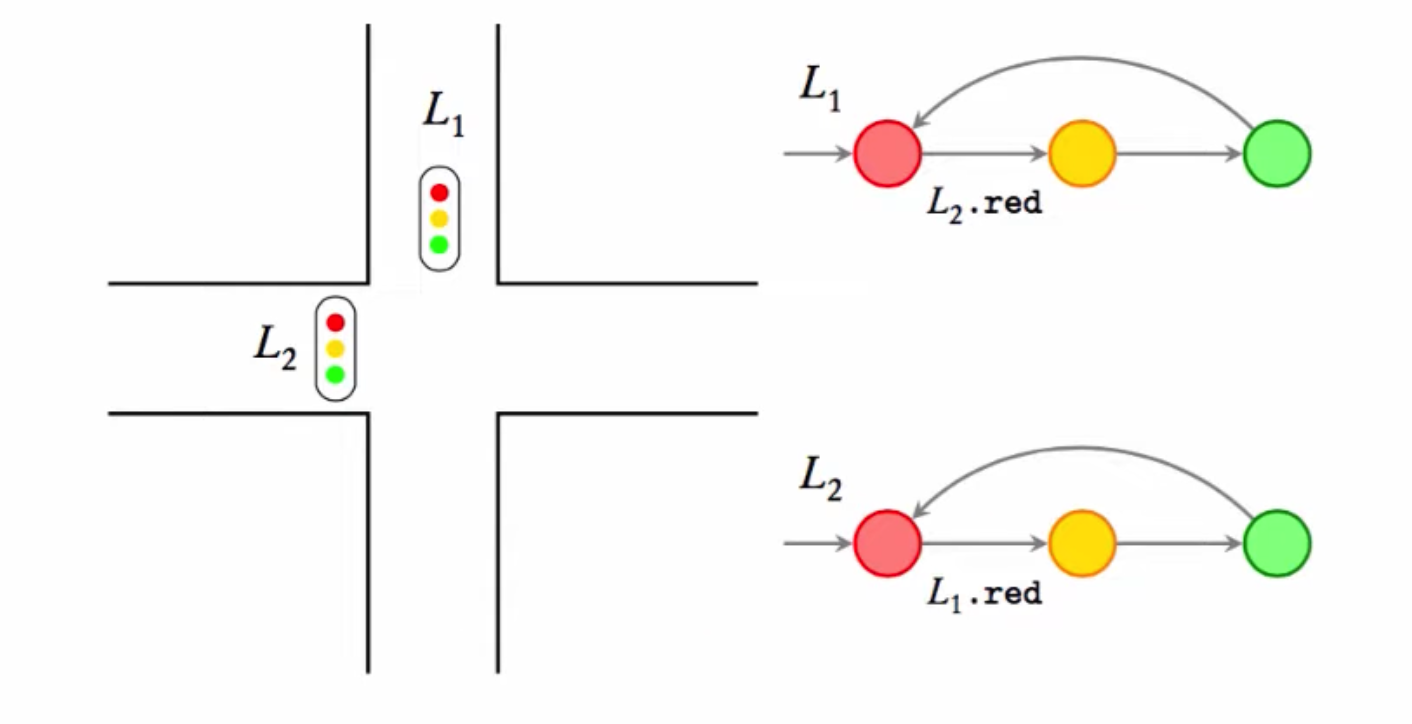
l1 and l2.red (r), yellow (y), green (g).red to yellow if the other light is red.red or green for arbitrary periods.yellow to green immediately in the next transition.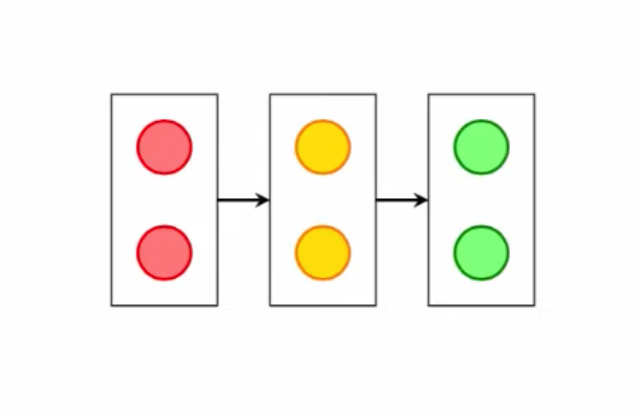
MODULE light(other)
VAR
state : {r, y, g};
ASSIGN
init(state) := r;
next(state) := case
state = r & other = r : {r, y};
state = y : g;
state = g : {g, r};
TRUE : state;
esac;
MODULE main
VAR
tl1 : light(tl2.state);
tl2 : light(tl1.state);
process keyword to declare asynchronous modules.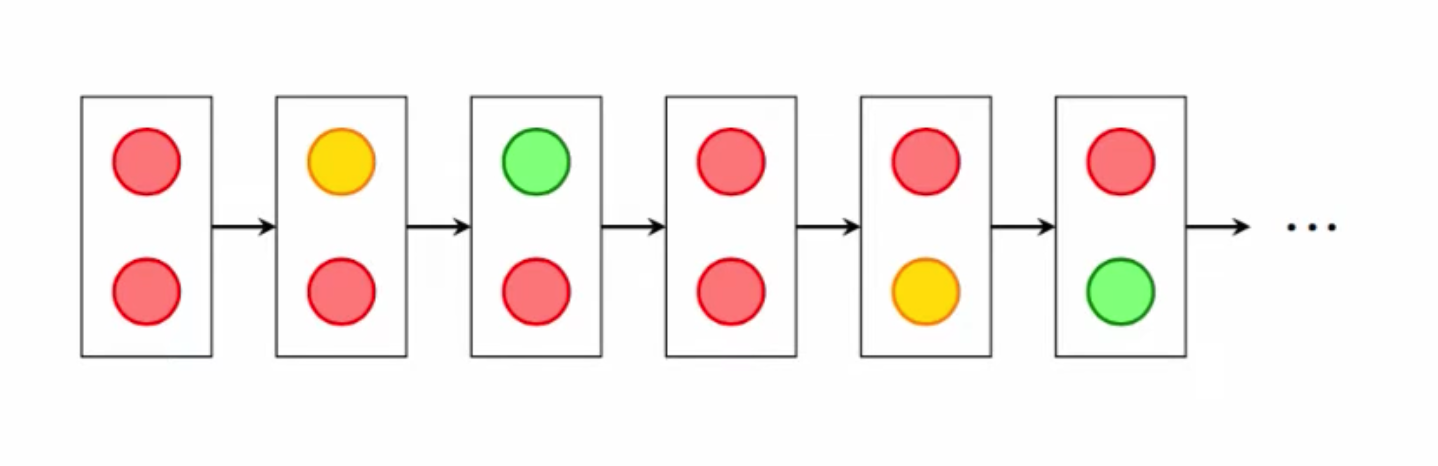
MODULE main
VAR
tl1 : process light(tl2.state);
tl2 : process light(tl1.state);
NuSMV -int light_asyn_demo.smv
go
check_ltlspec -p "!( F (tl1.state=g & tl2.state = g))
-Property checked: Never both green simultaneously.
print_reachable_states -v
pick_state -i
simulate -i -k 3
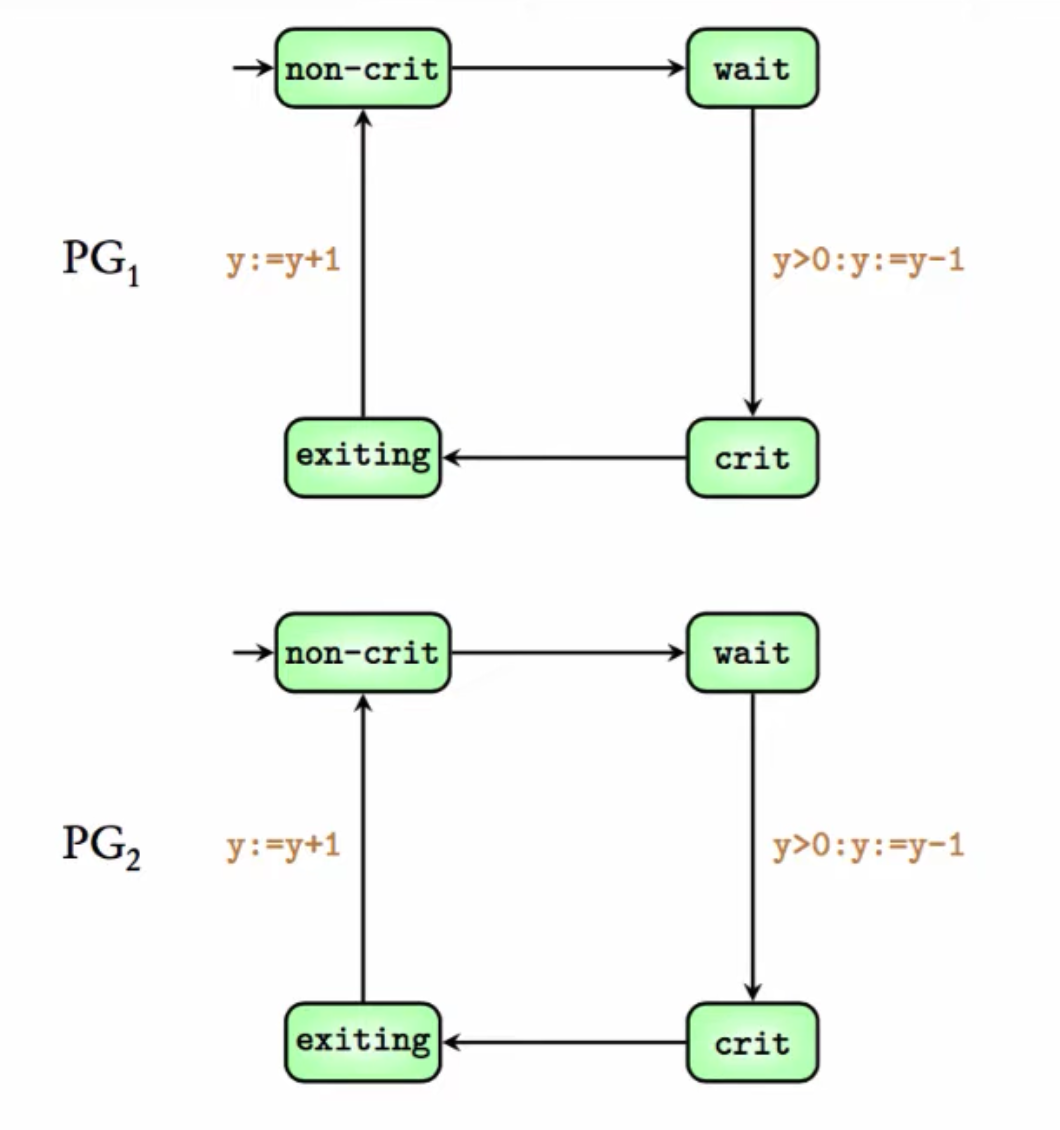
MODULE thread(y)
VAR
location : {nc, w, c, e};
ASSIGN
init(location) := nc;
next(location) := case
location = nc : {nc, w};
location = w & y > 0 : c;
location = c : {c, e};
location = e : nc;
TRUE : location;
esac;
next(y) := case
location = w & y > 0 : y - 1;
location = e & y = 0 : y + 1;
TRUE : y;
esac;
MODULE main
VAR
ymain : 0..1;
p1 : process thread(ymain);
p2 : process thread(ymain);
ASSIGN
init(ymain) := 1;
Two parallel programs sharing a resource.
y (0 or 1) controls access.y > 0, decrementing y.y is incremented.NuSMV -int mutex_demo1.smv
go
check_ltlspec -p "!F(p1.location=c & p2.location=c)"
pick_state -i
simulate -i -k 3
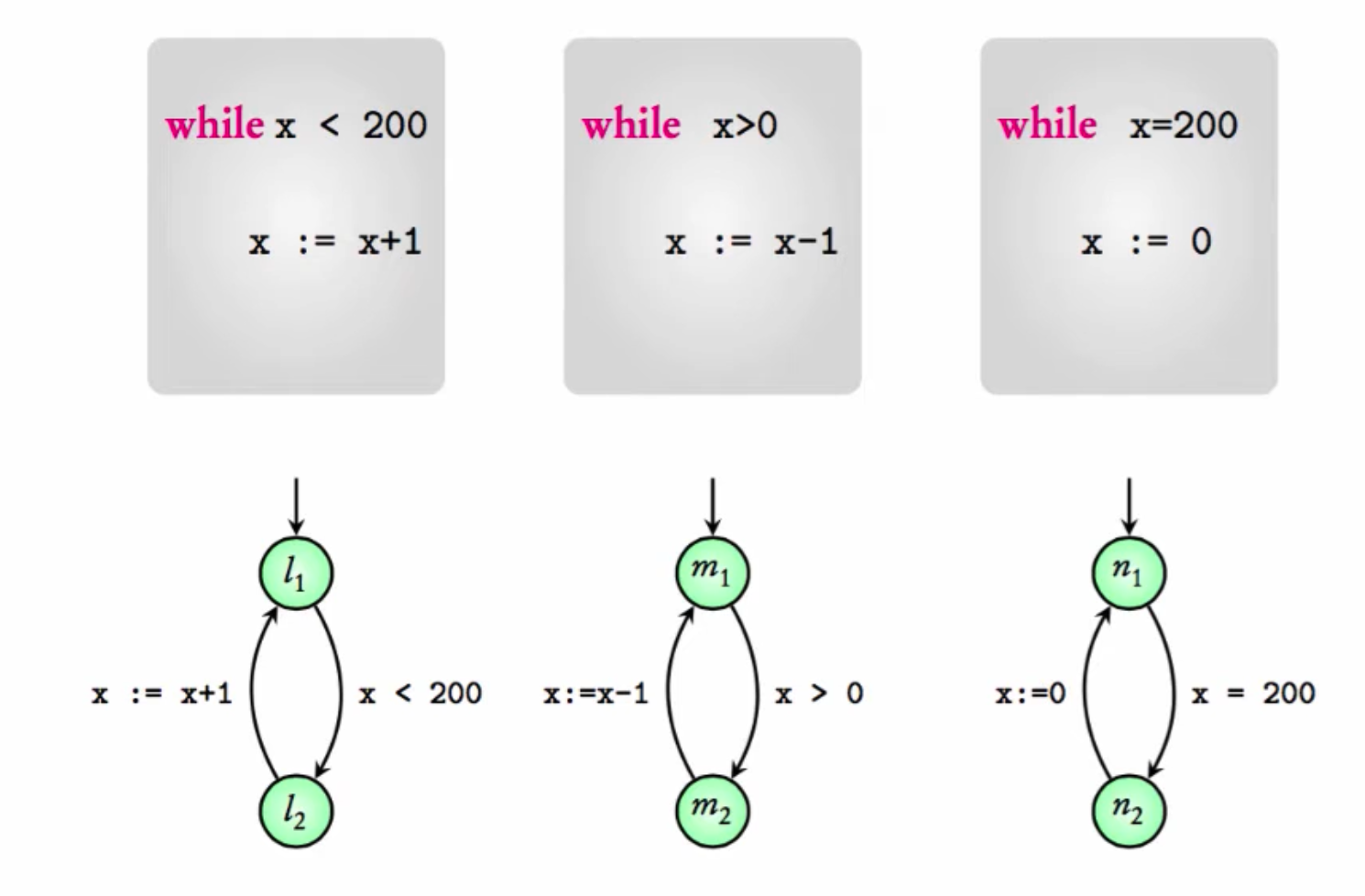
x (bounded between -1000 and 1000).MODULE program1(x)
VAR
location : {l1, l2};
ASSIGN
init(location) := l1;
next(location) := case
location = l1 & x < 200 : l2;
location = l2 : l1;
TRUE : location;
esac;
next(x) := case
location = l2 & x < 1000 : x + 1;
TRUE : x;
esac;
MODULE program2(x)
VAR
location : {m1, m2};
ASSIGN
init(location) := m1;
next(location) := case
location = m1 & x > 0 : m2;
location = m2 : m1;
TRUE : location;
esac;
next(x) := case
location = m2 & x > -1000 : x - 1;
TRUE : x;
esac;
MODULE program3(x)
VAR
location : {n1, n2};
ASSIGN
init(location) := n1;
next(location) := case
location = n1 & x = 200 : n2;
location = n2 : n1;
TRUE : location;
esac;
next(x) := case
location = n2 : 0;
TRUE : x;
esac;
MODULE main
VAR
x : -1000..1000;
thread1 : process program1(x);
thread2 : process program2(x);
thread3 : process program3(x);
ASSIGN
init(x) := 0;
NuSMV -int three_program_demo.smv
go
check_ltlspec -p "G (x>=0)"
x always non-negative.false with a counterexample where x becomes negative due to interleaving of increments and decrements.x = -1.process keyword.